原文地址：这里，省略了一些非重点片段。

尽管目前大多数系统都是通过gRPC或HTTP进行通信的，但仍有相当多的应用程序使用自定义协议。而且这些自定义协议中的许多都没有类似net/http这样方便的包来管理TCP连接。

这篇文章是为了那些直接和TCP连接打交道的人准备的。本文将讨论如何长期维护健康的TCP会话，以及如何对操持长链接的系统进行调优。

话不多说，先上图：

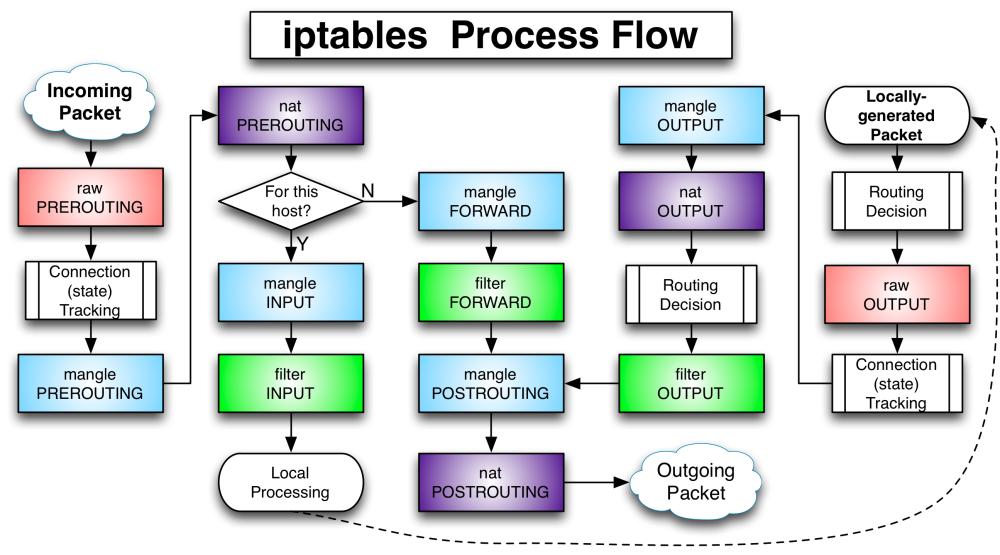
上图中的渐变色分别代表了iptables中的4个表：raw、nat、mangle、filter。按照功能来看：

• filter:负责过滤，防火墙。
• nat:网络地址转换功能，也就是network address translate。
• mangle:拆解报文，做出修改，并重新封装。
• raw:关闭nat表上启用的连接追踪机制。

未完待续…… 参考链接 libbpf HOWTO: BCC to libbpf conversion

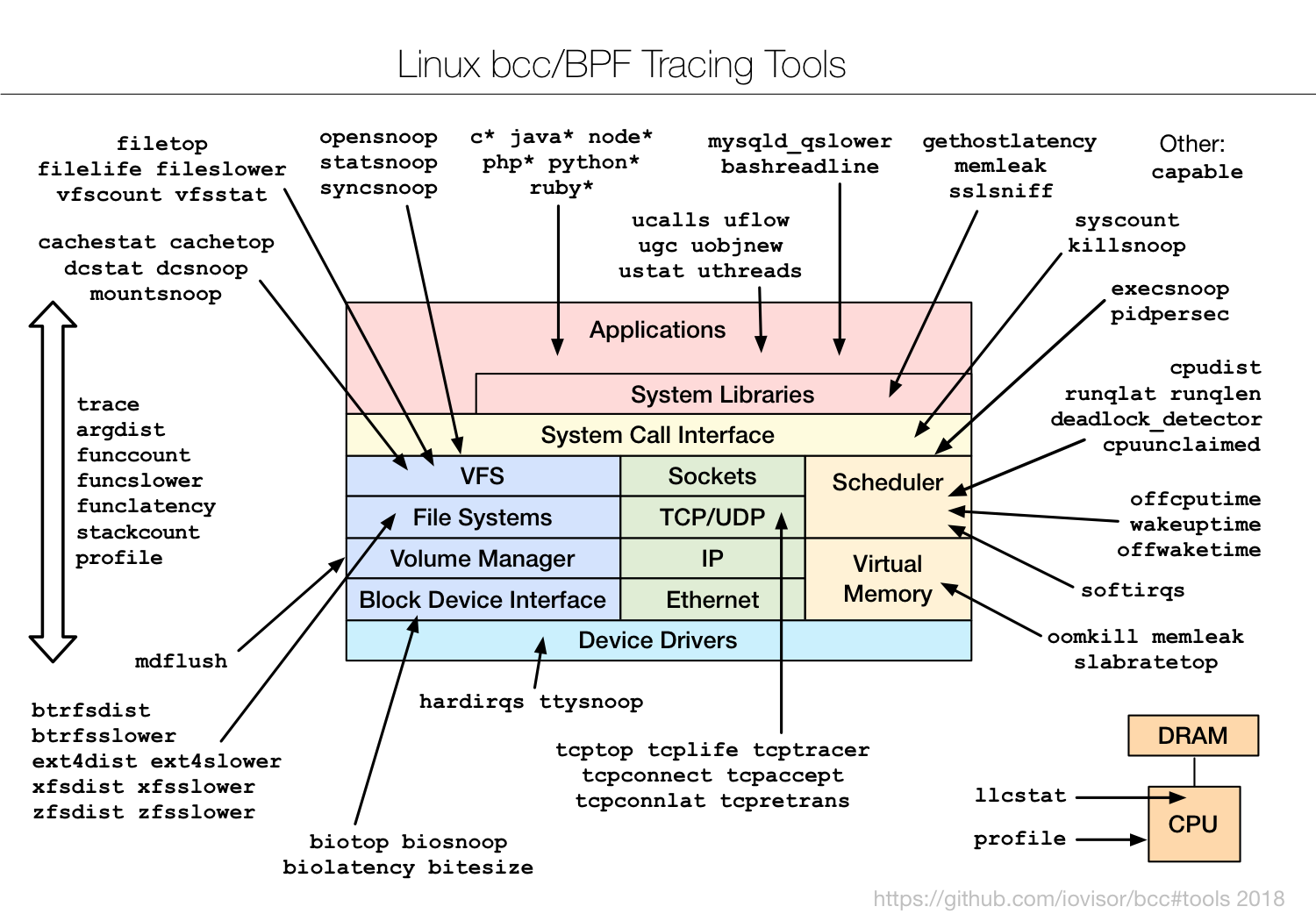
上一篇文章记录了如何使用bpftrace来编写bpf程序，这篇就来说说如何使用BCC(BPF Compiler Collection)。正如前一篇笔记说的，bpftrace简单是简单，但是对于某些复杂场景功能还略有不足。比如，很多的Linux工具都支持各种各样的参数，这时bpftrace就不能满足需求了。

如图所示，BCC已经提供了大量的二进制工具可以直接使用，这篇笔记主要侧重于如何使用BCC编写eBPF程序。

这篇文章主要来说说bpftrace，这个语法十分的简单而且功能还在不停的完善中，后续变化一定以官网文档为准。

基本语法

bpftrace程序由3个部分组成：

探针probes /过滤器filters/ {动作actions}

既可以把程序保存为.bt文件后（建议而不强制）使用btftrace xxx.bt来执行，也可以通过单行指令bpftrace -e 'probes /filters/ { actions }'来执行。

其中，过滤器部分可以省略掉，不省略的话只有符合过滤器条件时才会执行动作。

支持?::三元操作符、if{...}else{...}语句、unroll (count) {statements}这种有界的循环、while (condition) {...}(5.3+内核版本添加的实验性支持)、[]数组、(,)元组、以及C语言中的常见运算符。

上一篇笔记里说编写运行BPF程序推荐2种方法：bpftrace和BCC，按照惯例来个hello world。

之前说过很多功能都是新版内核才支持，想使用CO-RE内核需要开启CONFIG_DEBUG_INFO_BTF=y和CONFIG_DEBUG_INFO=y 这两个编译选项，所以建议使用最新的发行版，比如：

• Ubuntu 20.10+
• Fedora 31+
• RHEL 8.2+
• Debian 11+